Mihin episyklisiä vaihteita käytetään?

Episykliset vaihteettunnetaan myös planeettavaihteistojärjestelminä, ja niitä käytetään laajalti eri teollisuudenaloilla niiden kompaktin rakenteen, korkean hyötysuhteen ja monipuolisuuden ansiosta.

Näitä vaihteita käytetään pääasiassa sovelluksissa, joissa tila on rajallinen, mutta suuri vääntömomentti ja nopeuden vaihtelu ovat välttämättömiä.

1. Autojen vaihteistot: Episykliset vaihteet ovat automaattivaihteistojen avainkomponentteja, jotka mahdollistavat saumattomat vaihteenvaihdot, suuren vääntömomentin alhaisilla nopeuksilla ja tehokkaan voimansiirron.
2. Teollisuuskoneet: Niitä käytetään raskaissa koneissa, koska ne pystyvät käsittelemään suuria kuormia, jakamaan vääntömomentin tasaisesti ja toimimaan tehokkaasti kompakteissa tiloissa.
3. Ilmailu: Näillä vaihteilla on ratkaiseva rooli lentokoneiden moottoreissa ja helikopterien roottoreissa, sillä ne varmistavat luotettavuuden ja tarkan liikkeenohjauksen vaativissa olosuhteissa.
4. Robotiikka ja automaatio: Robotiikassa käytetään episyklisiä vaihteita tarkan liikkeenohjauksen, kompaktin rakenteen ja suuren vääntömomentin saavuttamiseksi rajoitetuissa tiloissa.

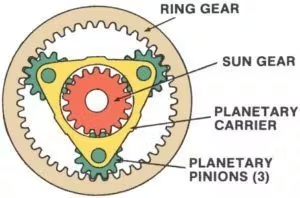
Mitkä ovat episyklisen vaihdelaatikon neljä elementtiä?

Episyklinen vaihdelaatikko, joka tunnetaan myös nimelläplaneettavaihteisto järjestelmä on erittäin tehokas ja kompakti mekanismi, jota käytetään yleisesti autojen vaihteistoissa, robotiikassa ja teollisuuskoneissa. Tämä järjestelmä koostuu neljästä keskeisestä elementistä:

1. Sun GearAurinkopyörä: Vaihteiston keskellä sijaitseva aurinkopyörä on liikkeen ensisijainen ajuri tai vastaanottaja. Se on suoraan yhteydessä planeettapyöriin ja toimii usein järjestelmän tulo- tai lähtölaitteena.

2. PlaneettapyörätNämä ovat useita hammaspyöriä, jotka pyörivät aurinkopyörän ympäri. Planeettapyörän kannattimeen asennettuna ne ovat kytkeytyneet sekä aurinkopyörään että kehäpyörään. Planeettapyörät jakavat kuorman tasaisesti, minkä ansiosta järjestelmä pystyy käsittelemään suurta vääntömomenttia.

3.PlaneetankantajaTämä komponentti pitää planeettapyörät paikoillaan ja tukee niiden pyörimistä aurinkopyörän ympäri. Planeetan kantolaite voi toimia tulo-, lähtö- tai kiinteänä elementtinä järjestelmän kokoonpanosta riippuen.

4.RengasvaihdeTämä on suuri ulkopyörä, joka ympäröi planeettapyörät. Kehäpyörän sisähampaat ovat kosketuksissa planeettapyörän kanssa. Kuten muutkin osat, kehäpyörä voi toimia tulo- tai lähtöpyöränä tai pysyä paikallaan.

Näiden neljän elementin vuorovaikutus tarjoaa joustavuutta erilaisten nopeussuhteiden ja suunnanmuutosten saavuttamiseen kompaktissa rakenteessa.

Kuinka laskea välityssuhde episyklisessä vaihdelaatikossa?

Vaihdevälityssuhdeepisyklinen vaihdesarja riippuu kiinteistä komponenteista, syötteestä ja lähdöstä. Tässä on vaiheittainen opas välityssuhteen laskemiseen:

1. Ymmärrä järjestelmän kokoonpano:

Tunnista, mikä alkuaine (aurinko, planeetankantoaine tai rengas) on paikallaan.

Määritä tulo- ja lähtökomponentit.

2. Käytä perusvälityssuhdeyhtälöä: Episyklisen vaihdejärjestelmän välityssuhde voidaan laskea seuraavasti:

GR = 1 + (R / S)

Jossa:

GR = Vaihdesuhde

R = Hammaskehän hampaiden lukumäärä

S = Aurinkopyörän hampaiden lukumäärä

Tämä yhtälö pätee, kun planeettakantaja on lähtö ja joko aurinko tai hammaspyörä on paikallaan.

3. Säädä muita kokoonpanoja varten:

• Jos aurinkopyörä on paikallaan, järjestelmän lähtönopeuteen vaikuttaa kehäpyörän ja planeettapyörän välityssuhde.
• Jos kehäpyörä on paikallaan, lähtönopeus määräytyy aurinkopyörän ja planeettapyörän välisen suhteen mukaan.

4. Peruutusvaihteen välityssuhde ulostulosta sisääntuloon: Nopeuden vähennystä laskettaessa (tulo suurempi kuin lähtö) välityssuhde on yksinkertainen. Nopeuden kertomista varten (lähtö suurempi kuin tulo) käännä laskettu välityssuhde.

Esimerkkilaskelma:

Oletetaan, että vaihdelaatikolla on:

Hammaskehä (R): 72 hammasta

Aurinkopyörä (S): 24 hammasta

Jos planeetan kantaja on lähtö ja aurinkopyörä on paikallaan, välityssuhde on:

GR = 1 + (72/24) GR = 1 + 3 = 4

Tämä tarkoittaa, että lähtönopeus on neljä kertaa hitaampi kuin syöttönopeus, jolloin alennussuhde on 4:1.

Näiden periaatteiden ymmärtäminen antaa insinööreille mahdollisuuden suunnitella tehokkaita ja monipuolisia järjestelmiä, jotka on räätälöity tiettyihin sovelluksiin.